前言
B+树是一种平衡树结构,在数据库索引和文件系统中有着广泛的应用。由于其高效的查询、插入、删除性能,B+树成为了众多数据结构的首选。本文将详细介绍B+树的结构和特性,并解释其在数据库索引中的实际应用和优势,帮助读者深入理解B+树的工作原理及其重要性。
B+ 树的基本概念和特点
B+ 树(B+ Tree)是一种常见的多叉树数据结构,用于在计算机科学领域中高效地组织和管理大量的有序数据。它在数据库管理系统、文件系统以及其他需要高效数据存储和检索的应用中广泛使用。B+ 树通过优化磁盘 I/O 访问和范围查询操作,使其成为处理大型数据集的理想选择。
B+ 树的基本概念
1. 多叉树结构: B+ 树是一种多叉树,其每个节点可以拥有多个子节点。相比于二叉树,B+ 树的分支更多,能够更高效地组织大量的数据。
2. 节点类型: B+ 树的节点分为内部节点和叶节点。内部节点用于索引和导航,而叶节点存储实际的数据。所有叶节点被连接成一个有序的链表,便于范围查询操作。
3. 排序和平衡: B+ 树要求其内部节点的子节点保持有序。而且,B+ 树保持严格的平衡性,即所有叶节点到根节点的距离相等,这确保了在查询过程中的高效性能。
4. 数据存储: 实际的数据存储在 B+ 树的叶节点上,而内部节点仅存储用于导航的索引键。这种设计使得 B+ 树的高度相对较低,从而减少了磁盘 I/O 操作。
5. 范围查询优化: 由于 B+ 树的叶节点形成有序链表,范围查询操作变得非常高效。通过遍历这个链表,可以快速检索位于某个范围内的数据。
6. 分裂与合并: 在插入操作中,当一个叶节点已满时,会触发分裂操作,将部分数据和索引移到一个新的叶节点中。而在删除操作中,如果一个叶节点的数据过少,可能会触发合并操作,将数据从一个叶节点移动到相邻的叶节点中。
7. 应用领域: B+ 树在数据库管理系统中常用作索引结构,可以加速数据库的查询操作。它还在文件系统中用于维护文件的索引,以及在键值存储系统中用于高效地存储和检索键值对数据。
8. 变体和扩展: B+ 树的变体包括 B* 树、Bx 树等,这些变体对于特定应用场景进行了优化,例如减少分裂操作次数或者提高范围查询的性能。
B+ 树相对于 B 树的特点
1. 更适合磁盘存储: B+ 树在设计上更加适合磁盘存储,这是由于其叶节点存储了实际的数据,而内部节点仅存储索引键。相比之下,B 树的每个节点都存储了数据,导致一次磁盘 I/O 读取的数据量较大。B+ 树的叶节点形成有序链表,使得范围查询时可以进行连续的磁盘读取,从而降低了 I/O 操作次数,提高了磁盘存储的效率。
2. 范围查询更高效: 由于 B+ 树的叶节点形成有序链表,范围查询操作变得高效。当需要检索某个范围内的数据时,只需从链表中的一个叶节点开始,连续遍历即可获取所需的数据,无需随机访问。而在 B 树中,不同叶节点可能分布在不同的层级,导致范围查询需要在不同的层级之间进行跳跃,增加了随机访问的成本。
3. 更稠密的索引: B+ 树通过在内部节点仅存储索引键,而将数据存储在叶节点中,使得每个节点可以容纳更多的索引键。这使得 B+ 树的高度相对较低,减少了磁盘 I/O 次数,提高了检索性能。
4. 有利于维护平衡: B+ 树在插入和删除操作时更容易维护平衡。由于 B+ 树的数据仅存储在叶节点中,节点的分裂和合并操作不会影响到其他内部节点。这与 B 树不同,B 树的节点既存储索引键又存储数据,导致插入和删除可能引起连锁反应,影响整体平衡。
5. 更稳定的性能: 由于 B+ 树在范围查询和磁盘 I/O 方面的优势,其性能在大多数情况下更加稳定。B 树在数据量较小时可能会退化成链表,导致性能下降,而 B+ 树由于其有序叶节点链表,避免了这种问题。
结构和组织
B+ 树的结构
1. 根节点(Root Node): 根节点是 B+ 树的顶层节点,是整个树的起始点。根节点可能具有不同的孩子节点数目(分支数),但它通常是一个中间节点,用于导航到更深层的节点。根节点存储的是索引键(或范围)和指向下一层节点的指针。
2. 中间节点(Internal Node): 中间节点位于根节点和叶节点之间,负责维护 B+ 树的索引结构。每个中间节点都包含一组索引键,这些索引键用于分隔其子节点中存储的数据范围。中间节点的子节点可以是另一个中间节点或叶节点。中间节点不存储实际的数据,只存储索引键和指向子节点的指针。
3. 叶节点(Leaf Node): 叶节点是 B+ 树中最底层的节点,存储了实际的数据。叶节点之间通过指针形成一个有序链表,使得范围查询变得高效。每个叶节点包含了一个或多个数据项,通常是键值对。叶节点的键值按照从小到大的顺序排列,形成了有序的数据序列。
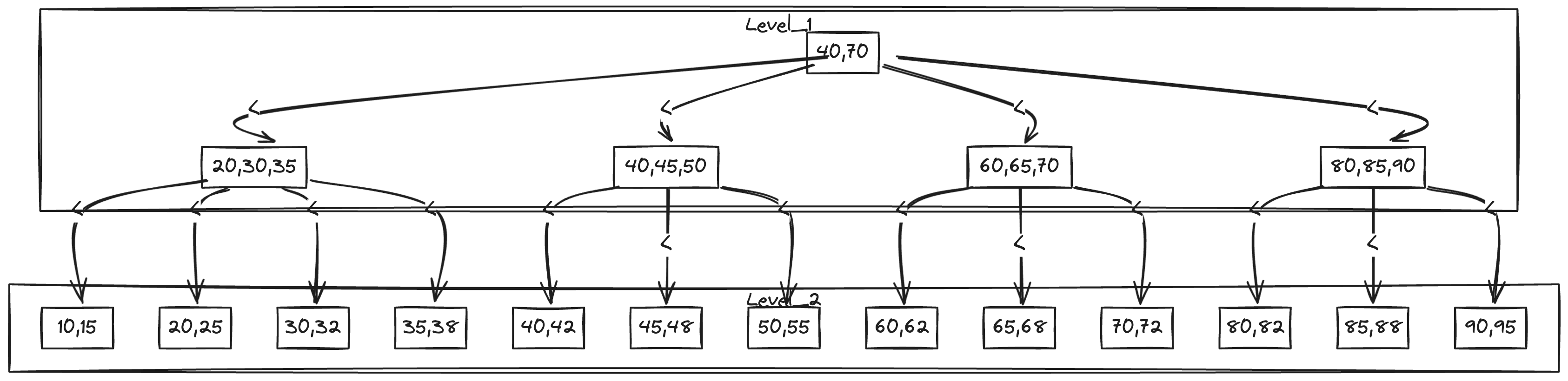
[根节点]
/ / \ \
[中间节点] [中间节点] [中间节点] ...
/ | \ / | \ / | \
[叶节点] [叶节点] [叶节点] [叶节点] [叶节点] ...
B+ 树的每个节点包含的键值和子节点数量都受到树的度数(或称分支因子)的限制。这个度数通常是一个固定的常数,它决定了每个节点可以包含的最大键值数量以及子节点数量。这种结构和限制保证了 B+ 树的平衡性,提高了查询和插入、删除操作的效率。
为什么 B+ 树的叶节点存储了实际数据,而中间节点用于索引和导航
B+ 树的叶节点是存储实际数据的地方。对于数据库管理系统、文件系统等应用,数据的实际内容就存储在这些叶节点中。每个叶节点可以容纳多个数据项,通常是键值对,其中键是用于检索数据的索引,而值则是实际存储的数据内容。叶节点按照从小到大的顺序排列,形成一个有序链表,使得范围查询非常高效。
中间节点在 B+ 树中用于导航和索引。每个中间节点存储一组索引键,这些键用于分隔其子节点存储的数据范围。通过这些索引键,B+ 树能够快速定位到叶节点中包含所需数据的范围。中间节点不存储实际数据,仅存储用于指引下一层节点的指针。这种设计保持了树的结构,确保了 B+ 树的平衡性,从而提高了检索和插入、删除操作的性能。
在范围查询中,通过在中间节点上的索引键,B+ 树可以迅速定位到叶节点的有序链表的起点,从而只需顺序遍历链表即可获得所需范围内的数据。这比在非叶节点上进行跳跃遍历更加高效,因为磁盘 I/O 通常是一个昂贵的操作,连续读取在性能上更加优越。
插入和删除操作
插入操作:
- 定位叶节点: 首先,根据插入的键值,从根节点开始向下导航,直到达到一个叶节点。这个叶节点将成为插入数据的位置。
- 插入数据项: 在叶节点中插入新的数据项(键值对)。如果叶节点未满,直接插入即可。如果叶节点已满,执行下一步。
- 叶节点分裂: 当叶节点已满时,执行叶节点的分裂操作。分裂会将节点的数据项分为两部分,一部分保留在原节点,另一部分移动到一个新创建的叶节点。分裂后,需要更新父节点中的索引键。
- 父节点处理: 如果分裂导致父节点也需要插入新的索引键,就按照索引键的大小将新索引键插入到父节点。如果父节点也满了,可能会继续向上递归执行分裂操作。
删除操作:
- 定位叶节点: 与插入类似,首先从根节点开始向下导航,找到包含待删除键值的叶节点。
- 删除数据项: 在叶节点中删除包含待删除键值的数据项。如果删除后叶节点的数据数量仍在合理范围内,操作完成。如果删除后节点过少,执行下一步。
- 叶节点合并: 当叶节点的数据项数量过少时,可以考虑将其与相邻的兄弟节点合并。合并会将两个节点的数据项合并为一个节点,同时更新父节点中的索引键。
- 父节点处理: 合并可能导致父节点中的索引键数量过少。如果父节点过少,可能需要继续向上递归执行删除操作,以保持平衡。
- 讨论插入和删除对树的平衡性的影响,以及如何通过调整维护平衡。
注意事项:
- 插入和删除操作可能会涉及多个节点的变动,所以需要确保操作过程中保持 B+ 树的平衡性。
- 节点的分裂和合并操作旨在保持树的平衡性,使得树的高度相对较低,从而提高检索性能。
- 在分裂和合并过程中,可能需要调整父节点和祖先节点中的索引键,以保证树的有序性。
搜索和范围查询
如何利用 B+ 树进行高效的搜索操作
1. 定位叶节点: 从根节点开始,根据要搜索的键值依次向下导航,直到达到一个叶节点。这个叶节点中存储了数据,可以根据数据项的键值大小快速找到目标数据。
2. 范围查询: 由于 B+ 树中的叶节点形成了有序链表,可以很容易地进行范围查询。如果需要查找一个范围内的数据,只需从叶节点的链表中的一个节点开始,连续遍历链表即可。由于有序性,无需进行随机访问,而是顺序地获取数据,从而提高了查询效率。
3. 二分查找: 在叶节点内部,可以使用二分查找来快速定位目标数据。由于叶节点内的数据是有序的,二分查找可以在 O(log n) 的时间内找到目标数据项,其中 n 是叶节点内的数据项数量。
4. 磁盘 I/O 优化: B+ 树的结构使得数据访问更加连续。在磁盘存储中,连续读取的效率通常比随机读取高,因为磁盘可以更有效地预取连续的数据块。B+ 树的叶节点存储在连续的磁盘块中,因此搜索操作会产生更少的磁盘 I/O 操作,从而提高检索效率。
B+ 树在范围查询中的优势
1. 数据都在叶节点上: B+ 树的叶节点是存储实际数据的地方,而中间节点仅存储索引键和子节点的指针。这意味着在进行范围查询时,只需遍历叶节点上的数据,无需考虑中间节点。这减少了不必要的数据访问,从而提高了范围查询的效率。
2. 有序链表: B+ 树的叶节点之间通过指针形成了一个有序链表,其中的数据项按照从小到大的顺序排列。这种有序性使得范围查询非常高效。从链表的一个叶节点开始,只需连续遍历链表中的数据项,即可获取所需范围内的数据。这减少了随机访问,提高了查询效率。
3. 连续磁盘读取: 由于叶节点数据在磁盘上连续存储,范围查询操作通常会涉及到连续的磁盘读取。磁盘对连续数据块的预取效率较高,因此 B+ 树在范围查询时可以更快地扫描数据,减少了磁盘 I/O 的成本。
4. 避免跳跃访问: 相比其他树结构,B+ 树在范围查询时不需要进行跳跃访问。即使查询范围跨越了多个叶节点,由于链表的连续性,可以按照顺序遍历数据项,而无需频繁地在不同节点之间跳跃。这有助于降低访问延迟。
磁盘 I/O 优化
B+ 树在磁盘存储上的优势
1. 顺序访问: B+ 树的叶节点存储在磁盘上的连续块中,这使得范围查询和顺序访问数据非常高效。当执行范围查询时,只需从链表的一个叶节点开始,连续地访问数据,从而充分利用了磁盘的顺序读取能力。相比于随机访问,顺序访问可以大幅提高数据读取速度。
2. 减少随机磁盘 I/O: B+ 树的设计目标之一是最小化磁盘 I/O 操作。叶节点的连续存储和链表形成确保了范围查询可以利用连续的磁盘块,从而减少了磁盘 I/O 操作。相比于随机访问的情况,B+ 树的结构使得数据读取更加紧凑,从而减少了磁盘寻址的开销。
3. 磁盘预取优势: 由于 B+ 树的叶节点数据在磁盘上连续存储,磁盘驱动器可以利用预取(prefetching)策略,提前加载相邻的数据块到内存中。这种顺序性可以最大程度地利用磁盘驱动器的缓存和预读能力,进一步提高读取速度。
4. 最小化随机访问延迟: 随机磁盘 I/O 往往会引入较大的延迟,因为需要进行磁盘寻址和旋转等操作。B+ 树的设计目标是尽量减少随机访问,通过顺序访问的方式来优化数据的检索。这样可以显著降低数据访问的延迟,提升整体性能。
5. 更少的磁盘碎片: 由于 B+ 树的节点结构和分裂合并策略,它能够在维护树的平衡性的同时减少磁盘碎片的产生。相比于其他树结构,B+ 树能更好地保持节点的连续存储,减少了因碎片而导致的额外读取成本。
如何利用 B+ 树的结构减少磁盘寻址次数,提高数据检索性能
1. 顺序性和范围查询: B+ 树的叶节点存储在磁盘上的连续块中,并形成了有序链表。这使得范围查询可以高效地顺序访问数据,从而减少了随机访问和磁盘寻址的次数。通过优化查询计划,尽量进行范围查询,可以充分利用这种有序性。
2. 利用磁盘预取: 由于 B+ 树叶节点的有序性,磁盘驱动器可以利用预取(prefetching)策略,提前将相邻的数据块加载到内存中。这样,当需要访问相邻的数据块时,可能已经在内存中,从而减少了磁盘寻址的延迟。
3. 最佳节点容量选择: 在设计 B+ 树时,选择适当的节点容量可以影响磁盘寻址次数。节点容量过小会导致树过深,增加寻址次数。节点容量过大可能导致节点内数据过于稀疏,影响磁盘的空间利用率。通过权衡节点容量,可以达到较好的性能平衡。
4. 局部性原理: B+ 树的结构遵循局部性原理。当访问一个节点时,其相邻节点的访问可能也会在近期内发生,因为节点之间有着相对紧密的联系。这意味着磁盘寻址很可能会被缓存的热数据击中,从而减少了磁盘 I/O 操作。
5. 节点分裂和合并的影响: 节点的分裂和合并操作会影响 B+ 树的平衡和结构。这些操作的目标是保持树的平衡,从而保证树的高度较低。合适的节点分裂和合并策略可以减少不必要的磁盘寻址,确保树的性能。
数据库和文件系统中的应用
B+ 树在数据库管理系统和文件系统中的广泛应用
数据库管理系统中的应用:
- 索引结构: 数据库管理系统广泛使用 B+ 树作为索引结构,用于加速数据的检索操作。数据库中的表数据通常会根据某个列的值进行索引,B+ 树能够快速定位到存储着所需数据的叶节点,从而加速查询操作。
- 范围查询: 数据库中的范围查询操作非常常见,B+ 树在这方面的优势得到了充分的发挥。B+ 树的有序性和顺序访问特点使得范围查询操作非常高效,这在数据库中的许多应用场景中是关键需求。
- 连接操作: 在连接(JOIN)操作中,B+ 树可以用于实现连接条件的匹配。通过对连接列创建索引,可以加速连接操作的执行,提高数据库的查询性能。
- 唯一性约束: 数据库表中的唯一性约束可以通过 B+ 树的唯一索引来实现。B+ 树的结构保证了唯一性,这可以在插入数据时避免重复值的出现。
文件系统中的应用:
- 文件索引: 文件系统使用 B+ 树作为文件的索引结构,以便快速定位到文件的数据块。B+ 树的结构能够在文件系统中维护文件的层次结构,使得文件的检索和访问更加高效。
- 空间管理: 文件系统需要管理存储空间的分配和回收。B+ 树可以用于跟踪文件和存储块之间的映射关系,以及存储块的使用情况,从而实现高效的空间管理。
- 日志管理: B+ 树可以被用于管理文件系统的日志,记录文件和数据块的变化。这样可以在文件系统发生崩溃或错误时,恢复文件系统到一致的状态。
B+ 树如何帮助管理大规模数据和支持高效查询
1. 存储效率: B+ 树的节点结构和分裂合并策略使得树的高度相对较低,从而减少了磁盘 I/O 操作。这对于大规模数据的管理非常关键,因为磁盘 I/O 通常是性能瓶颈。B+ 树的设计在存储上更加紧凑,能够高效地存储大量数据。
2. 顺序性和范围查询: B+ 树的叶节点形成了有序链表,使得范围查询非常高效。在大规模数据中,范围查询是常见的需求,B+ 树通过顺序访问和链表的优势,能够快速返回所需的数据范围,而不需要额外的随机访问。
3. 磁盘预取: 由于 B+ 树的顺序性,磁盘驱动器可以利用预取策略,提前加载相邻的数据块到内存中。这在处理大规模数据时尤为有利,可以最大程度地利用磁盘驱动器的缓存和预读能力,降低磁盘 I/O 延迟。
4. 分布式数据存储: 对于分布式数据存储系统,B+ 树可以用于建立索引,跨越多个存储节点。这样可以在大规模数据集中实现分布式查询,每个节点负责一部分数据,同时利用 B+ 树的结构加速查询。
5. 内存和缓存利用: B+ 树的有序性和层次结构使其适合内存和缓存的利用。在大规模数据情况下,数据通常不可能全部载入内存,B+ 树的设计允许在内存中维护树的部分节点,仍然能够高效执行查询。
6. 支持高并发: 在数据库管理系统中,高并发是常见的场景。B+ 树的设计和分层结构允许多个查询同时进行,而不会出现锁竞争等问题,从而支持高并发的查询操作。
缓存和内存优化
B+ 树在内存中的应用,如何利用缓存来加速查询
1. 内存中的 B+ 树优势: 在内存中存储 B+ 树具有以下优势:
- 快速访问: 内存读取速度远高于磁盘读取,可以实现几乎实时的数据访问。
- 无磁盘 I/O 延迟: 在内存中的数据无需经过磁盘 I/O 操作,避免了磁盘寻址和旋转等延迟。
- 随机访问性能提升: 内存中的随机访问远比磁盘上的随机访问快,因此 B+ 树内存中的节点可以更迅速地访问。
2. 利用缓存加速查询: 在内存中的 B+ 树可以通过合理地利用缓存来进一步提高查询操作的效率:
- 页缓存: 数据库管理系统和文件系统通常会使用页缓存,将部分 B+ 树节点保留在内存中,以便在查询操作中快速访问。缓存可以避免频繁的磁盘读取,提高查询性能。
- 热数据缓存: 根据局部性原理,访问的数据可能会在近期内再次访问。通过缓存热数据,可以减少相同数据的多次磁盘读取,进一步加速查询。
- 查询结果缓存: 对于一些频繁的查询,可以将查询结果缓存到内存中。这样,当相同的查询再次出现时,可以直接从缓存中获取结果,无需再次执行查询操作。
3. 缓存管理和清理策略: 缓存的管理和清理也是关键。一些策略可以帮助优化内存中 B+ 树的性能:
- LRU(最近最少使用)策略: 将最近被访问过的节点保留在缓存中,淘汰最久未使用的节点。这有助于保持热数据在缓存中,提高访问速度。
- 缓存预加载: 在查询开始之前,可以预先加载查询可能用到的节点到缓存中,以减少查询时的磁盘访问。
- 合理设置缓存大小: 缓存大小应该根据系统内存的大小和应用的需求来设置,避免过大导致内存不足,也避免过小影响性能。
LRU(最近最少使用)等缓存替换策略在 B+ 树中的作用
1. 热数据保留: 在 B+ 树的内存中,经常被访问的节点是热数据,它们很可能在不久的将来再次被访问。LRU 缓存替换策略允许保留最近被访问过的节点,从而优先保留热数据,加速查询操作。这对于频繁访问的 B+ 树节点非常有益。
2. 提高数据访问速度: LRU 等缓存替换策略有助于将频繁访问的节点保留在内存中,减少了从磁盘中读取数据的次数。这使得 B+ 树的节点可以更快地被访问,提高了数据的访问速度,从而加速查询操作。
3. 避免频繁磁盘 I/O: LRU 策略可以减少不必要的磁盘 I/O 操作。如果热数据得到保留,可以避免频繁地从磁盘中读取相同的数据,从而降低了磁盘寻址和数据传输的延迟。
4. 缓解内存压力: B+ 树可能会涉及大量节点,但内存是有限的。LRU 策略有助于管理内存,使其只保存最有用的数据。这有助于缓解内存压力,保证重要的数据能够在内存中得到充分利用。
5. 合理权衡: 尽管 LRU 在保留热数据方面表现出色,但对于冷数据(不常访问的数据)可能会频繁地被淘汰出缓存。在某些情况下,可能需要根据实际应用场景权衡不同的缓存替换策略,例如,可以根据数据的重要性和访问频率来调整缓存策略。
B+ 树与其他常见的数据结构(如平衡二叉树、哈希表等)比较
B+ 树:
- 优势:
- 适用于范围查询: B+ 树的有序性和叶节点的有序链表使得范围查询非常高效。
- 支持顺序访问: 有序性使得顺序访问和范围查询在 B+ 树中表现出色。
- 适合磁盘存储: B+ 树的结构和磁盘 I/O 优化使其非常适合处理大规模有序数据。
- 平衡性: B+ 树通过节点分裂和合并来保持平衡,从而维护了较低的树高度。
- 适用场景:
- 数据库管理系统: 用于索引和范围查询,适合存储大规模有序数据。
- 文件系统: 用于文件索引,支持文件的快速检索。
- 分布式系统: 在分布式环境中,B+ 树可以支持分布式数据存储和查询。
平衡二叉树(如 AVL 树、红黑树):
- 优势:
- 更紧凑: 平衡二叉树的高度相对较低,适用于内存中的数据结构。
- 更灵活的操作: 平衡二叉树的插入和删除操作相对更灵活,可能会导致更少的节点分裂和合并操作。
- 适用场景:
- 内存中的索引: 对于小规模数据集,或需要频繁插入和删除操作的场景,平衡二叉树更为合适。
- 有限的范围查询: 平衡二叉树也能支持范围查询,但在有大量有序数据时,B+ 树更为高效。
哈希表:
- 优势:
- O(1) 的平均查找时间: 哈希表的查找操作通常在平均情况下具有常数时间复杂度。
- 适合键值对存储: 哈希表适合存储关联的键值对,如缓存、哈希集合等。
- 适用场景:
- 快速查找: 需要快速查找特定键的值时,哈希表是不错的选择。
- 缓存: 哈希表适用于缓存数据,以快速响应对已知键的查询请求。
总结:
- B+ 树适合大规模有序数据的存储和范围查询,尤其在数据库和文件系统中表现出色。
- 平衡二叉树适合内存中的索引,支持较小数据集或需要频繁的插入和删除操作。
- 哈希表适合快速查找和键值对存储,特别是需要 O(1) 平均查找时间的情况。
B+ 树在实际系统中的应用
1. 数据库索引: B+ 树在数据库管理系统中广泛应用于索引结构,用于加速数据的检索操作。例如,MySQL 等关系型数据库系统使用 B+ 树作为索引结构,通过在 B+ 树上构建索引,可以快速定位到所需数据。
2. 文件系统: 文件系统使用 B+ 树作为文件的索引结构,以便快速定位到文件的数据块。在 Linux 的 Ext4 文件系统中,B+ 树被用于管理文件的数据块和元数据,从而支持高效的文件存储和检索。
3. 键值存储: 键值存储引擎,如 Redis 和 RocksDB,也使用 B+ 树作为其底层存储结构。这些存储引擎使用 B+ 树来管理键值对的存储和查询,以及支持范围查询和排序等操作。
4. 分布式存储系统: 在分布式存储系统中,B+ 树可以用于构建分布式索引,使得数据分布在多个节点上。这样可以支持分布式数据的存储和查询,同时充分利用 B+ 树的优势。
5. 数据库查询优化: 数据库查询优化器可以使用 B+ 树的索引信息来选择最优的查询计划,以减少磁盘 I/O 和提高查询性能。B+ 树的有序性和范围查询优势使其在查询优化中发挥重要作用。
6. 时间序列数据库: 时间序列数据库用于存储和查询按时间顺序排列的数据,如传感器数据、日志等。B+ 树的有序性和范围查询特性使其适合处理时间序列数据。
7. 存储引擎: 许多数据库管理系统的存储引擎,如 InnoDB、MyRocks 等,使用 B+ 树作为底层存储结构。这些存储引擎能够处理大规模数据,并支持高效的事务处理。
B+ 树的变体和扩展
1. B* 树: B* 树是 B+ 树的一种变体,其主要目标是进一步减少中间节点的数量,提高树的填充度。在 B* 树中,中间节点至少填充到半满。与 B+ 树不同,B* 树不会在中间节点上存储数据,而只存储索引。这样可以提高数据在叶节点上的紧凑性,减少磁盘 I/O 操作。
适用场景: B* 树适合磁盘存储场景,特别是需要进一步减少磁盘 I/O 操作的情况。它在数据库和文件系统中可以用于更好地优化磁盘访问模式。
2. Bx 树: Bx 树是 B+ 树的另一种变体,它是一种多维的扩展,用于支持多维数据的存储和查询。Bx 树在每个节点上使用多个键值来对数据进行排序,以支持多个维度的查询。Bx 树的每个维度类似于一个独立的 B+ 树。
适用场景: Bx 树适用于多维数据的存储和查询,如地理信息系统(GIS)、数据仓库等。它能够高效地处理多维数据的范围查询和过滤操作。
3. B-link 树: B-link 树是 B+ 树的另一种变体,它专注于提高内存中 B+ 树的查询性能。在 B-link 树中,只有叶节点包含数据,内部节点仅包含索引和指向下一级叶节点的指针,这使得 B-link 树具有更浅的高度,进而加快了查询速度。
适用场景: B-link 树适合内存中的索引结构,特别是在查询速度和内存利用率之间需要取得平衡的情况。
4. Bω树: Bω树是一种变体,旨在解决 B+ 树中频繁的节点分裂和合并问题。Bω树允许每个节点的关键数目在一定范围内变化,而不是固定的。这样可以降低树的维护开销。
适用场景: Bω树适用于需要降低树结构维护开销的情况,可以减少频繁的节点分裂和合并操作。
总结
B+树作为一种高效的数据结构,凭借其平衡性和有序性,显著提高了数据的查询和管理效率。通过本文的介绍,读者可以了解到B+树的结构特点及其在数据库索引中的重要作用,进而更好地应用在实际开发中。
